Speeding up my AoC solution by a factor of 2700 with Dijkstra's
Note: this post contains spoilers for one of the days of Advent of Code 2021.
This article was discussed on Hacker News.
This year, I had a lot of fun with Advent of Code. There’s a nice problem solving aspect of it and refining your initial solution is always a fun exercise.
I do my solutions in Haskell, and AoC problems can be nice explorations into various performance-wise aspects of GHC’s runtime. My README has some notes on what my general approach is to getting programs to run faster.
But sometimes, you can get solutions that run orders of magnitude faster, and this year I encountered such a case where my solution ran over 2700 times faster! Let’s dive in.
A naïve attempt
Day 15 asks us to compute the
lowest sum possible that results from traversing a grid from one
corner to the other, where the possible moves are moving by one in the
four cardinal directions. When I saw this problem, I
thought, “this is just recursion!” Naturally, I wrote such a
recursive solution (glguy notes on IRC that this would be a lot faster
if I memoized the calls.) The base case is if we’re at the origin
point, the cost is 0. Otherwise, the minimum cost starting at (r,c)
is the cost of the cell at (r,c) added with the minimum of
recursively solving the same problem for (r-1,c), (r,c-1) and
(r,c+1).
import qualified Data.Map as M
minSum :: Int -> Int -> M.Map (Int, Int) Int -> Int
minSum r c g
| r == 0 || c == 0 = 0
| otherwise = g M.! (r, c) + minimum [minSum (r - 1) c g, minSum r (c - 1) g, minSum r (c + 1) g]
This was sufficient for the very small example they gave. But it fails even on part 1, which was a 100 by 100 grid! In fact, it is an incorrect solution as well (if we restrict the problem to only down and right moves then a dynamic programming solution would work.)
Clearly, even a naïve solution won’t save us here. The next approach
I went with uses Dijkstra’s
Algorithm. One
limitation I impose on myself in solving Advent of Code is to not use
any libraries outside the GHC bootstrap
libraries.
This is simply because in some environments such as Google Code Jam or
Codeforces, fancy libraries would not exist, but ones such as
containers certainly would be.
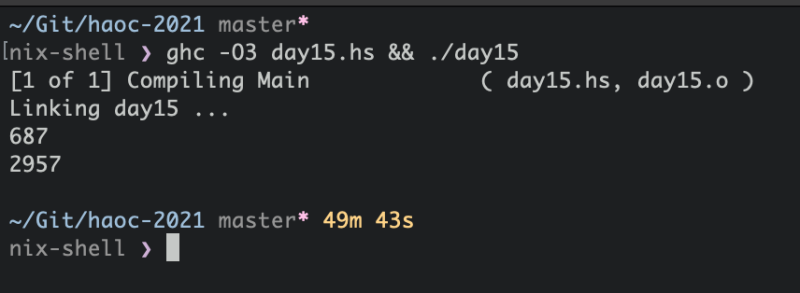
And sure enough, Dijkstra’s algorithm was able to solve part 1 in a few seconds. Part 2 however, just kept churning. I left my computer running then returned to see the result, which was accepted by the validator online. My shell also prints out how long the previous command took to execute, so that acted as a timer.
Finding cost centers
Even though we got the right answer, there’s no way that this is a reasonable runtime for a solution. To find the culprit, I ran the Haskell profiler on the program solving part 1.
COST CENTRE MODULE SRC %time %alloc
dijkstra.step3.nextVert.v.\ Main day15.hs:101:47-96 86.1 0.0
dijkstra.step3.nextVert.v Main day15.hs:101:13-128 11.8 28.2
...
The function to compute the next vertex to visit (see the pseudocode) by choosing vertex by minimum distance from source.
v :: (Int, Int)
v = minimumBy (\x y -> compare (dv M.! x) (dv M.! y)) q
where q is the set of vertices left to visit and dv is a map from
vertices to distances. Using minimumBy on a Set in Haskell calls
foldl' on sets, which is
here.
This procedure of course will be linear in the size of the set, and a
500 by 500 grid has 250,000 vertices to find the minimum of each time
we want to select another vertex. Yikes. I imagined, “what if we were
able to just find the next vertex of minimum distance from the source
in constant time?” Thus, we would be able to breeze through this part
of the algorithm and bring the runtime significantly down.
Priority queues from scratch
There’s a nice “duality” to the operation of Dijkstra’s algorithm when
you use a priority queue. You have a map where the keys are vertices
and the elements are distances, but when you select the next vertex to
visit, you use a priority queue where the keys (priorities) are
distances and the elements are vertices. The structure of each is
optimized for a different aspect of the algorithm, so conflating the
two would intuitively cause slowdown. With that in mind, we can
define a priority queue as just a map from Ints to lists of values
of that priority.
type PQueue a = IntMap [a]
Getting a next minimal element from the priority queue is easy, since
IntMaps already a provide a minViewWithKey function. Insertion is
similarly easy to write up. The empty priority queue is just an empty
IntMap.
-- Retrieve an element with the lowest priority
pminView :: PQueue a -> ((Key, a), PQueue a)
pminView p =
let Just (l, p') = IM.minViewWithKey p
in case l of
(_, []) -> pminView p'
(k, x : xs) -> ((k, x), if null xs then IM.delete k p' else IM.insert k xs p')
-- Insertion of an element with a specified priority
pins :: Int -> a -> PQueue a -> PQueue a
pins k x = IM.insertWith (++) k [x]
Note that pminView already returns the new map with the minimal
element removed, so we don’t need to write another deletion function.
With those functions in hand, and lots of rewriting, I finally cracked it!
Benchmarks!
The results were staggering—part 2 was sped up by a factor of 2545, which is a serious demonstration of how even if you have the right algorithm, the choice of how you represent auxillary data in the algorithm matters.
benchmarking day15/part2
time 1.172 s (1.088 s .. 1.259 s)
0.999 R² (0.997 R² .. 1.000 R²)
mean 1.213 s (1.190 s .. 1.244 s)
std dev 29.96 ms (12.16 ms .. 39.32 ms)
variance introduced by outliers: 19% (moderately inflated)
After checking the cost centers again, a small
adjustment
to how neighbors were computed reduced the mean running time to
1.098 seconds, which amounts to a 2716 times speedup!
Final thoughts
Not using premade libraries was a great pedagogical constraint because it forced me to get to the essence of an algorithm or data structure. While implementations of Dijkstra’s algorithm exists in various Haskell libraries, they are often too optimized or specialized to certain structures. There’s a lot to be learned from doing things from scratch!